IMU Noise Model
December 12, 2022
The IMU Noise Model
-
Kalibr에 사용된 IMU 측정 모델에는 두 가지 유형의 센서 오류가 포함되어 있음
-
White Noise- 매우 빠르게 변동하는 noise
-
Bias- 천천히 변동하는 센서 bias
-
예를 들어, 각도에 대한 rate measurement인 는 아래와 같이 표현 가능
- 세 개의 센서 축 모두를 모델링하기 위해 동일한 모델이 독립적으로 사용됨
- 위 모델은 가속도계 측정 오류를 모델링하는 데에도 사용되기도 함
-
White Noise
-
continuous-time
-
-
(noise strength)
⇒ 클수록 gyro measurements의 노이즈가 심함을 의미
⇒ :
gyroscope_noise_densityin Kalibr⇒ :
accelerometer_noise_densityin Kalibr
-
-
discrete-time
-
- : sampling time
-
Bias
- Brownian motion process, Wiener process, Random walk 등으로 불림
-
continuous-time
-
-
: white noise
⇒ 이 값은 bias의 strength와 결합되어 bias를 결정하게 됨
-
(gyro bias strength), (accel bias strength)
⇒ bias의 variations이 클수록 위 파라미터를 높게 설정해야 함
⇒ :
gyroscope_random_walkin Kalibr⇒ :
accelerometer_random_walkin Kalibr
-
-
-
discrete-time
-
The Noise Model Parameters in Kalibr
-
White Noise Model
| Parameter | Kalibr element | Symbol | Units |
|---|---|---|---|
| Gyroscope “white noise” | gyroscope_noise_density |
||
| Accelerometer “white noise” | accelerometer_noise_density |
||
| Gyroscope “random walk” | gyroscope_random_walk |
||
| Accelerometer “random walk” | accelerometer_random_walk |
||
| IMU sampling rate | update_rate |
How to Obtain the Parameters for your IMU
From the Datasheet of the IMU
- Check the Datesheet of the IMU
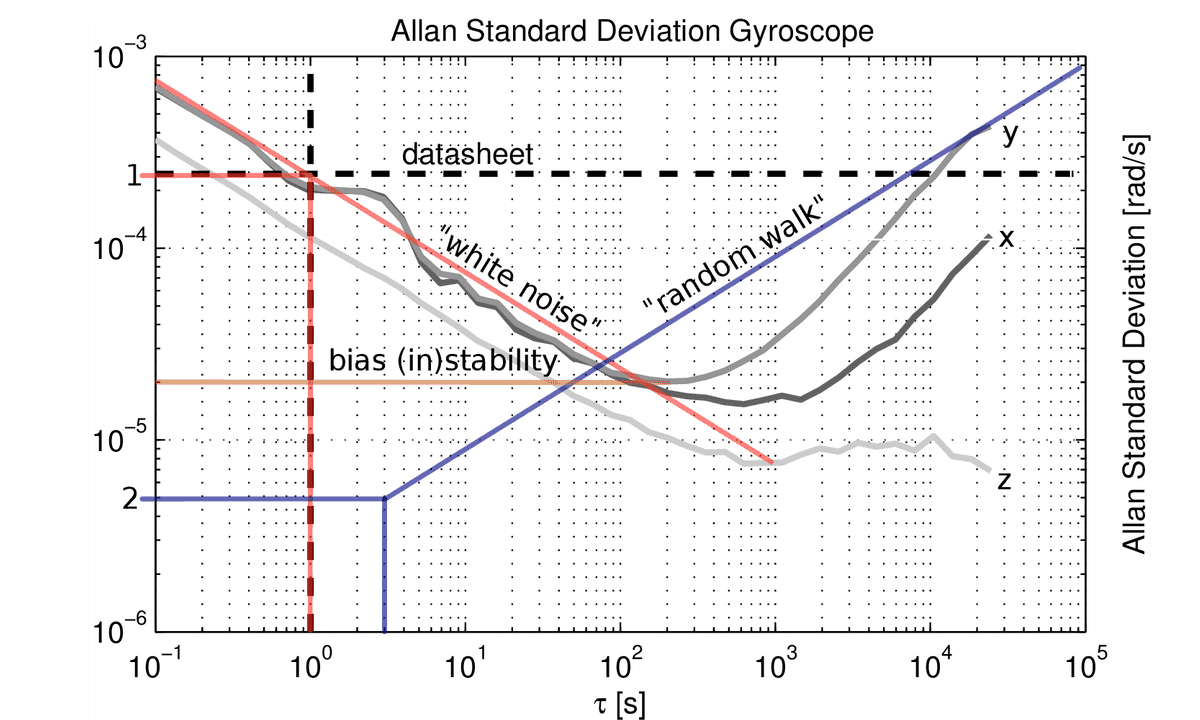
From the Allan standard deviation (AD)
-
The useful open source tool for computing IMU parameters using Allan Deviation
- Allan standard deviation of a MEMS gyro with manually identified noise processes